レッスン映像
06章01節…ばらつきの程度を示す指標「標準偏差」:STDEV.P関数
(01)以下のような表を作成しましょう。「選択式試験/記述式試験」のスコア一覧です。
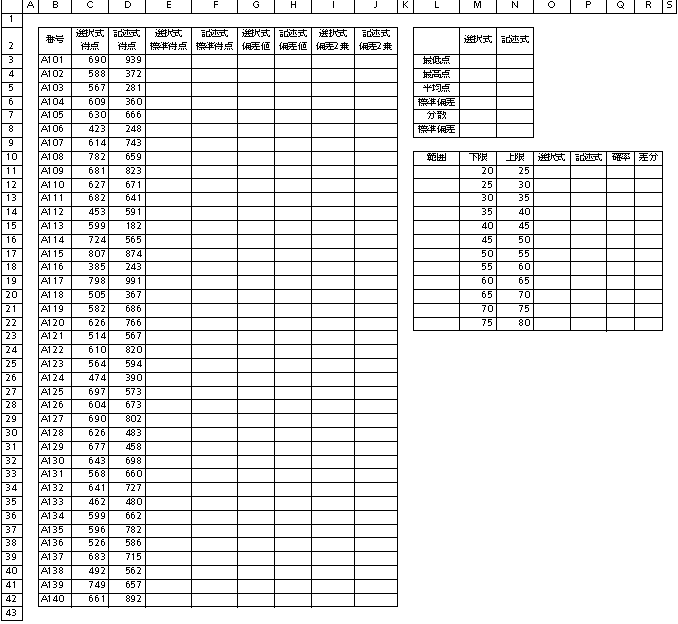
(02)M3:N5にて各試験の「最低点/最高点/平均点」を算出してください。
「平均点」は小数2桁まで表示させます。
(03)「選択式/記述式」の平均点は、おおよそ同じ値になりました。
(04)平均点はおおよそ同じですが、点数のばらつき具合に違いがありそうです。
以下は「階級幅:100単位」で作成したヒストグラムです。いずれにしても平均値の近辺を中心に値が集まっているようです。平均より離れた値の出現数は、なだらかに減っています(このような得点分布傾向を「正規分布」という)。両方の得点とも山型・凸型の分布をしています。[選択式得点]のほうが鋭い山型・凸型です。[選択式得点]のほうがばらつきが少ないといえます。
(05)平均からどの程度ばらけている値グループ・母集団なのか、を示すために使われる指標として「標準偏差」があります。「STEDEV.P」関数を使うことで値グループの標準偏差が算出できます。セルM6で「選択式得点」の[標準偏差]を求めます。
関数の作成を開始してください。
(06)[統計]もしくは[すべて表示]から「STDEV.P」関数を選択します。
値グループから「標準偏差」を求めることができます。
(07)[数値1]は「C3:C42」としてOKします。
(08)セルM6に作成した、標準偏差を求める式をN6へコピーしましょう。小数点以下の数値は2桁表示にします。数値の小さい「選択式」では平均値/中央に値が集まっている傾向があるようです。数値の大きい「記述式」では値がばらけている傾向があるようです。この数値は、次節にあるように値の出現率の推測に利用することができます。